![]()
210. 课程表 II
难度: 中等
来源: 每日一题 2023.09.10
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
- 例如,想要学习课程
0,你需要先完成课程1,我们用一个匹配来表示:[0,1]。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
示例 3:
输入:numCourses = 1, prerequisites = []
输出:[0]
提示:
1 <= numCourses <= 20000 <= prerequisites.length <= numCourses * (numCourses - 1)prerequisites[i].length == 20 <= ai, bi < numCoursesai != bi- 所有
[ai, bi]互不相同
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
}
}
分析与题解
-
深度优先遍历 + 环检测 + 拓扑
这个题目相对于昨天的题目, 主要的区别在于, 我们不但需要判断有向图的环的存在, 还需要返回顺序结构.
我做的过程中唯一想不明白的就是 如果
[[1, 2] [0, 2]]也就是 1 和 0 都遍历, 我们该怎么办? 假设先遍历1的邻接表, 再遍历2的邻接表.这时候, 遍历
1的邻接表resultList = [0 ,1]结构.这时候, 但是在遍历
2的邻接表的时候, 我们先前的结构难道需要重新构建吗 ?其实很简单, 根本不需要再次重新构建, 因为不管
[0, 1, 2]还是[0, 2, 1]还是说[0, 3, 4, 1, 2].只要保证 1 和 2 在 0之后, 1 和 2的顺序根本就无所谓!
了解完这个思路之后, 其他的和昨天的题目的解题思路一样即可, 只不过, 我们还需要构建一个
resultList, 用于存储结果.如何判断这些课程是否能够完成呢? 其实我们主要的依据就是 环, 就是图中有环存在, 例如下面几种情况.
-
两个课程相互依赖造成的环
-
多个课程的循环依赖造成的环
-
自己依赖自己造成的环
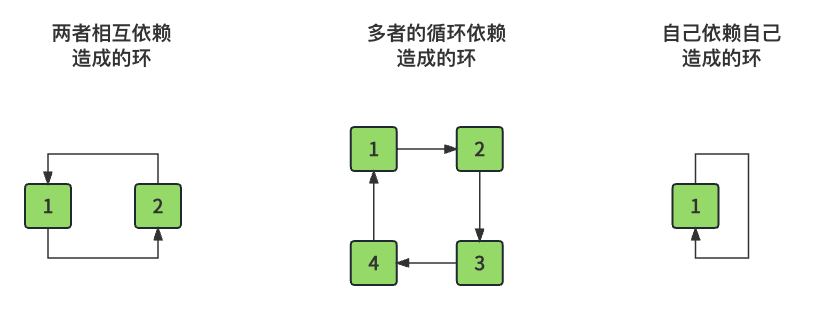
另外, 上面是各种环的情况, 但是我们该如何通过代码判断呢? 就是我们会在遍历的过程中把先前遍历的课程节点入栈, 当遍历过程中再次遇到相同的节点, 那就是存在环了, 直接停止遍历, 返回结果即可.
知道整体的解题方向了, 我们需要下面就说一下具体的解题过程.
首先, 我们还是要构建有向图的邻接表的结构.
// 创建图的邻接表 Map<Integer, List<Integer>> cache = new HashMap<>(); // 构建图的邻接表 for(int[] item : prerequisites) { if (cache.get(item[0]) == null) { cache.put(item[0], new ArrayList<Integer>()); } cache.get(item[0]).add(item[1]); }然后我们需要构建三个缓存结构
resultList、finding和finish,finding主要用于相当于在遍历过程中的入栈存储结构,finish主要存储已经遍历完成的结构的头节点, 当再次遇到就不需要遍历该结构了.List<Integer> resultList = new ArrayList<>(); Set<Integer> finish = new HashSet<Integer>(); Set<Integer> finding = new HashSet<Integer>();然后就是遍历整个邻接表, 同时利用
finish缓存减少遍历的次数.for(Integer key : cache.keySet()) { if (!finish.contains(course)) { if (!dfs(course, cache, resultList, finding, finish)) { return new int[0]; } } }在深度优先遍历
dfs方法中, 我们首先就是判断 当前节点是否遍历过(在finish数组中) 如果在查找栈中就直接停止了.if (finish.contains(courses)) { return true; } if (finding.contains(courses)) { return false; }如果上述条件都不满足, 那么就把当前的头部节点暂时放入
finding数组中. 然后就是查找他的邻接表数组, 如果找不到环, 就把移除finding.finding.add(course); List<Integer> result = cache.get(course); if (result != null) { for (Integer item: result) { if (!dfs(item, cache, resultList, finding, finish)) { return false; } } } finding.remove(course);如果上面查找不到环, 那就说明当前头部节点就是一条链路, 加入到
finish数组 和resultList数组中, 证明遍历过. 防止重复遍历, 并且返回 True 即可.resultList.add(course); finish.add(course); return true;把所有邻接表遍历完成之后, 我们是否还有别的遗漏呢? 答案当然是还有了, 那就是如果这节课根本没有依赖, 这时候, 我们就需要遍历一次,筛选出没有邻接表的元素, 当然了, 这个会导致运行时间变长,解决方案就是我们给每一个课程都创建一个邻接表, 不管它是否含有依赖.
for(int i = 0; i < numCourses; i++) { if (!finish.contains(i)) { resultList.add(i); } }最后, 我们构建我们的结果数组即可.
int[] result = new int[numCourses]; for(int i = 0; i < numCourses; i++) { result[i] = resultList.get(i); }接下来,我们看一下整体的解题思路如下所示.
class Solution { public int[] findOrder(int numCourses, int[][] prerequisites) { // 先构建邻接表 Map<Integer, List<Integer>> cache = new HashMap<>(); for(int[] item : prerequisites) { if (cache.get(item[0]) == null) { cache.put(item[0], new ArrayList<>()); } cache.get(item[0]).add(item[1]); } // 深度优先遍历所有课程 List<Integer> resultList = new ArrayList<>(); Set<Integer> finding = new HashSet<>(); Set<Integer> finish = new HashSet<>(); for(Integer course: cache.keySet()) { if (!finish.contains(course)) { if (!dfs(course, cache, resultList, finding, finish)) { return new int[0]; } } } for(int i = 0; i < numCourses; i++) { if (!finish.contains(i)) { resultList.add(i); } } int[] result = new int[numCourses]; for(int i = 0; i < numCourses; i++) { result[i] = resultList.get(i); } return result; } public boolean dfs(Integer course, Map<Integer, List<Integer>> cache, List<Integer> resultList, Set<Integer> finding, Set<Integer> finish) { if (finish.contains(course)) { // 如果还能进来, 那就说明遍历过, 已经添加到resultList中, 就不用遍历了 return true; } if (finding.contains(course)) { return false; } finding.add(course); List<Integer> result = cache.get(course); if (result != null) { for (Integer item: result) { if (!dfs(item, cache, resultList, finding, finish)) { return false; } } } finding.remove(course); resultList.add(course); finish.add(course); return true; } }
复杂度分析:
- 时间复杂度: O(n), 时间复杂度与所有课程节点的个数成线性关系.
- 空间复杂度: O(4n), 会创建三个空间
resultList、cache、finish以及finding, 每一个空间都与所有课程节点数成线性关系.
结果如下所示.

-







Comments | 0 条评论