
解析器概述
由于编译原理内容太过于枯燥, 所以当时我就在想能不能写一个编译过程, 这时候就在B站上看到了熊爷的技术去魅篇 - PrattParser解析器.
解析器主要的工作是把一系列的标记转换为树的表示形式. 例如线性代码 a = 1 + 1 * 3 的转换过程如下所示.
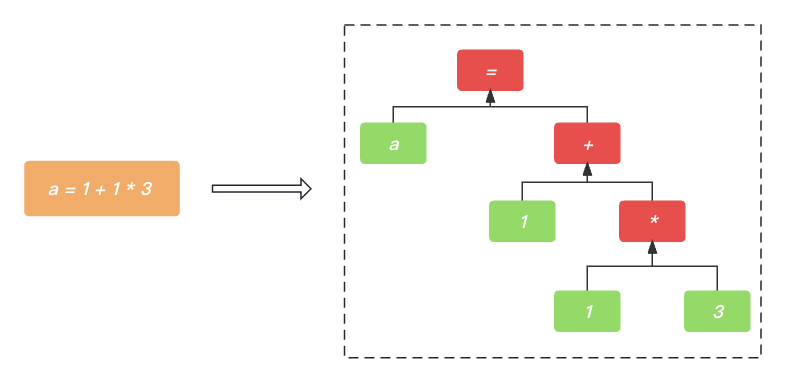
想要实现如下的转换过程, 我们一般需要实现解析器, 而想要实现解析器一般有两种方式.
-
使用 Parser generator (所有验证大部分来自CharGPT, 了解就好)
-
手工实现解析器
使用 Parser generator 进行上面的转换过程, 用一种DSL (例如 BNF ) 来描述你的语法, 这时候, a = 1 + 1 * 3 会变成什么样呢? 如下所示.
statement ::= expression_statement | assignment_statement
expression_statement ::= expression
assignment_statement ::= identifier '=' expression
expression ::= additive_expression
additive_expression ::= multiplicative_expression ( ('+' | '-') multiplicative_expression )*
multiplicative_expression ::= primary_expression ( ('*' | '/') primary_expression )*
primary_expression ::= number | identifier | '(' expression ')'
number ::= digit+
digit ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
identifier ::= letter (letter | digit)*
letter ::= 'a' | 'b' | 'c' | ... | 'y' | 'z' | 'A' | 'B' | 'C' | ... | 'Y' | 'Z'
看到这样的转换结果, 谁脑子不是嗡嗡的? 这还是最简单的赋值过程.
所以 BNF 虽然可以完成转换过程, 它的缺点也是很明显.
-
歧义性
BNF 描述的语法规则可能存在歧义。如果有多个不同的推导路径可以生成同一个句子,则称为文法歧义。在设计语言或编译器时,歧义性可能导致解析困难或语言不一致。
-
缺乏语义信息
BNF 只关注语法结构,而忽略了语义信息。它无法直接描述语义规则和操作。语义的处理往往需要通过其他方式来表示和处理。
-
粒度较粗
BNF 是一种上下文无关语法表示方法,它主要关注语法结构的形式化描述,而对于上下文相关的语法规则,如特定的运算顺序、关键字的语义等,BNF 的表达能力较弱。
-
可读性较差
BNF 使用了一些特殊的符号和记号,对于非专业人士来说,对于语法规则的理解可能具有一定的难度。此外,复杂的语法规则可能导致 BNF 的表示变得冗长和难以阅读。
-
不适合描述部分语言特性
BNF 对于一些编程语言中的特定特性,如正则表达式、回溯和优先级等的描述相对困难。对于一些复杂的语法规则,BNF 可能无法直接表示或需要引入扩展规则。
但是, 瑕不掩瑜, 尽管 BNF 存在这些缺点,但它仍然是一种被广泛应用于语言设计、编译器构建和形式语言的描述方法,它在建立语法基础和形式化验证方面仍然具有重要的作用。
对于手工实现解析器, 这里主要说的就是PrattParser解析器, 就是接下来, 我们一起看一下PrattParser解析器的相关内容.
PrattParser解析器概述
PrattParser解析器主要是对编译前端工作: 词法分析 、 语法分析 、 语义分析 、 中间代码生成 这几个部分的一个实践.
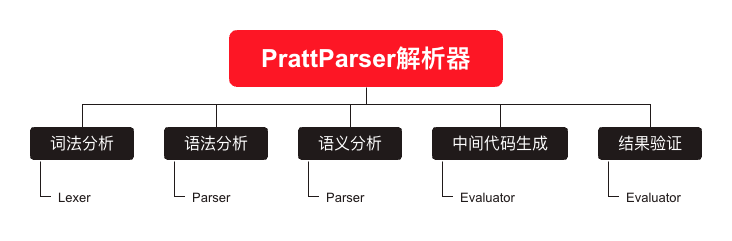
每一个过程, 我们会在后面的章节中进行探讨, 我们先聊一下 PrattParser解析器 生成 AST语法树 的理论支撑.
首先, 当一段代码通过 词法分析器 之后成为一个个Token词法单元, 这个过程看似简单, 实际上也是很简单, 枚举所有的符号, 移除所有的空格, 换行等, 就完成了这一过程. 具体如下所示.
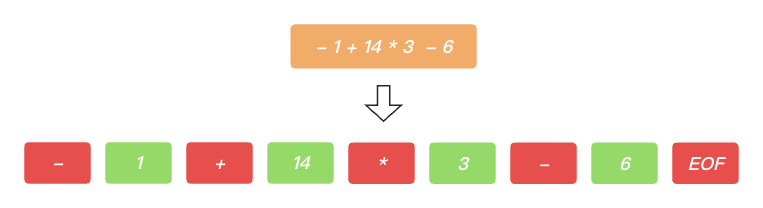
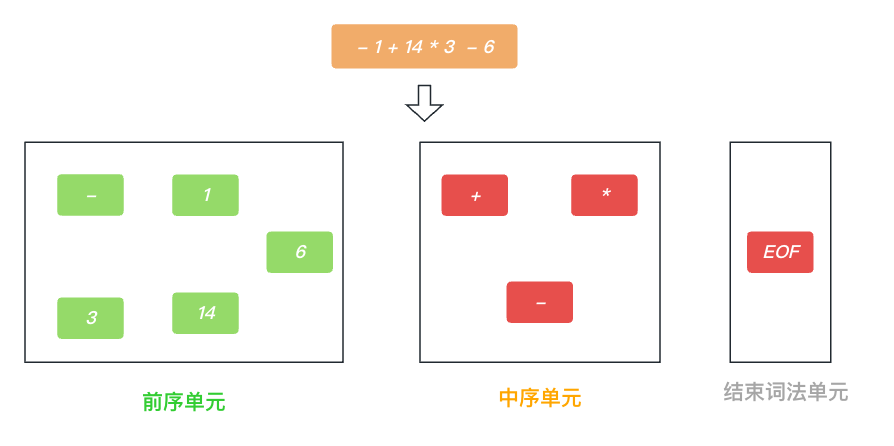
在 PrattParser解析器 中, 认为所有的词法单元Token只有两种类型 前序单元 和 中序单元.
在基础运算中, 我们可以认为 + - * / 是中序单元, 因为这种符号关联左边符号Token, 比如加法, 必然要有 a + b.
像 1 所有的数字都是前序单元, 同时还有一个特殊的前序单元 那就是 - 号, 也就是 - 号既可以是中序单元也可以是前序单元. +9 这种形式暂不讨论....
那么, PrattParser解析器 如何解决运算符的优先级的呢? 比如-1 + 14 * 3 - 6 正确的应该是 (-1 + (14 * 3))- 6 ✅, 而不是 (-1 + 14) * 3)- 6 ❎, 也就是生成的AST语法树的过程如下图所示.
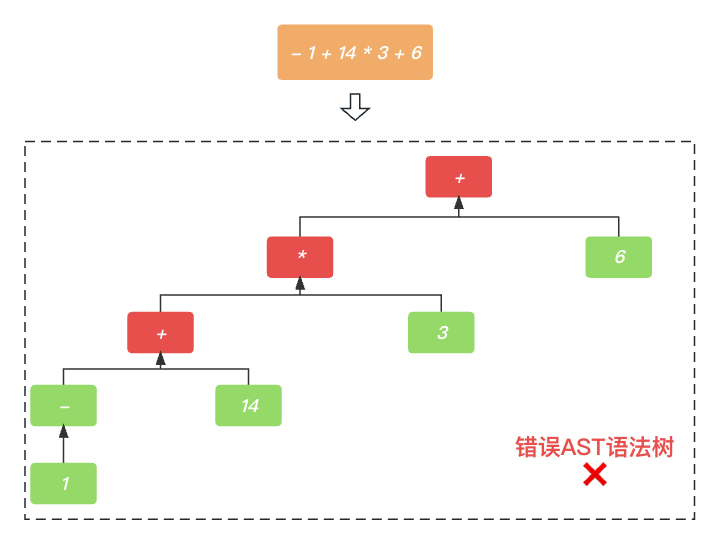
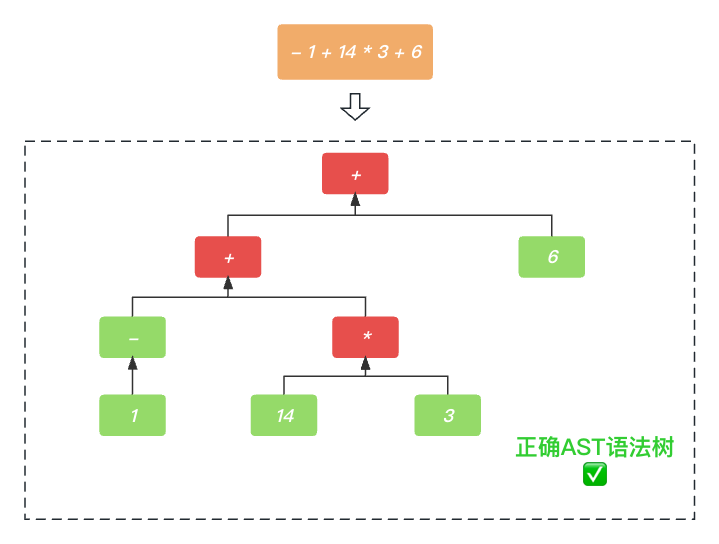
实际上, PrattParser解析器 解决运算符的优先级问题, 就是预设了每一种算数运算符的优先级. 优先级的定义也是根据数学运算中 先乘除后加减 的原则来的. 具体如下表所示.
| 符号单元 | 优先级 |
|---|---|
| NUM | 0 |
| + | 1 |
| - | 1 |
| * | 2 |
| / | 2 |
哪怕有这个表, 我们也是云里雾里的, 我们接下来就用最简单的示例 1 + 2 * 3 来演示 PrattParser解析器 是如何运用优先级生成 AST语法树的.
PrattParser解析器与AST语法树
对于 1 + 2 * 3 这个数学表达式来说. 我们需要通过 递归 构建整个AST语法树.
首先, 然后是通过 词法分析器 我们首先拆分成如下的 词法单元Token : 1 + 2 * 3 EOF
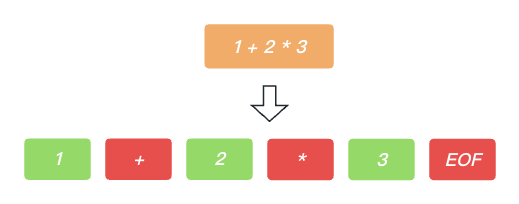
然后, 我们读取第一个词法单元 1. 并形成前序节点. 我们初始化当前表达式优先级为0(NUM).

然后我们读取下一个词法单元 +, 这时候, 我们发现 + 的优先级(1)要高于左边的优先级, 所以, 1 被 + 号吸引, 成为其左节点. 这时候整体优先级变成 1 .

+ 这个中序节点有了左节点, 那就需要去寻找它的右节点, 这时候找到了第二个数字词法单元 2, 本来到这里就结束了. 但是紧接着发现 2 后面跟的是 乘法词法单元 *, 如下图所示.
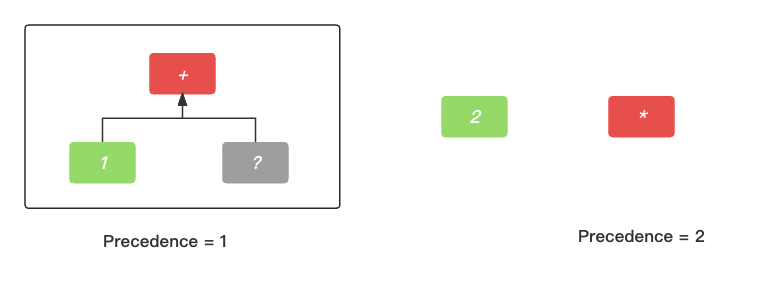
乘法词法单元 *优先级为 2, 比当前 + 号的优先级高, 所以它就会对数字词法单元 2更有吸引力, 所以 2 成为 * 的左节点. 而加号+ 的右节点的寻找过程只能继续等待了.
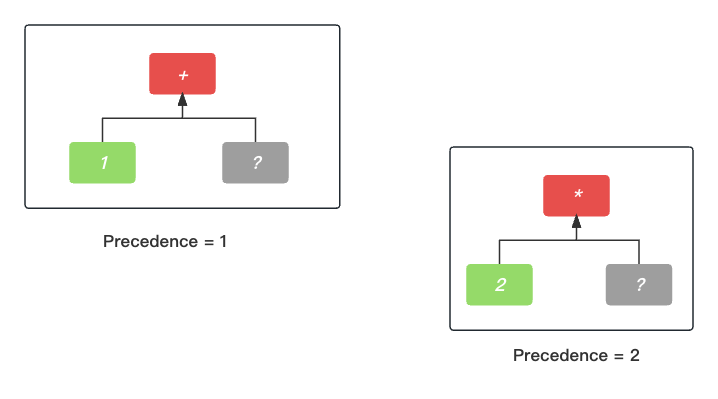
这时候, 加号+ 的右节点的寻找过程已经在暂停的路上(PS: 其实上是递归过程的递过程, 还没有进入归过程呢.), 我们要先解决乘法* 的右节点问题. 然后, 我们继续按照上面的思路寻找右节点, 发现了数字词法单元3, 再往后一个单元就是结束词法单元EOF了.
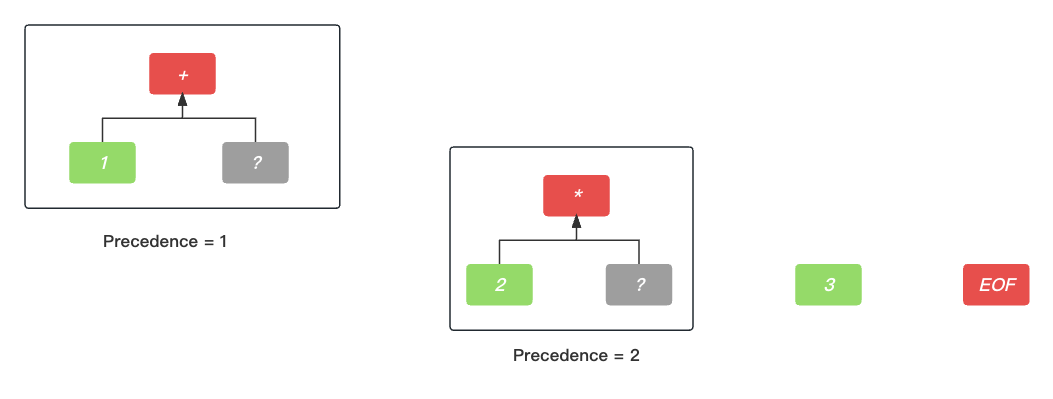
不用说了, 碰到结束词法单元EOF, 我们就直接构建根节点为乘法*的AST语法树.
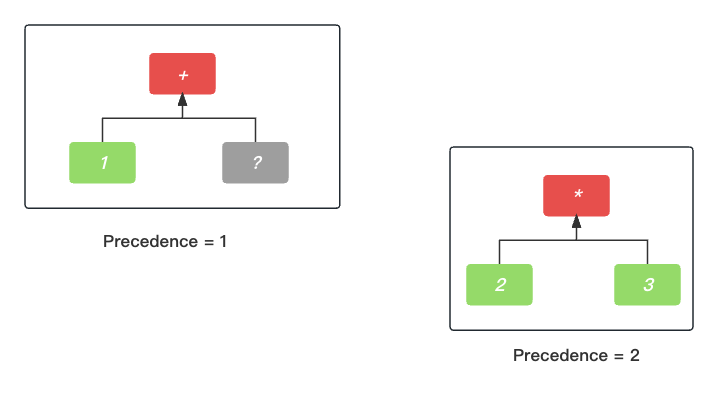
然后, 对于 加号节点+ 的右节点寻找过程来说, 也进行了递归的归过程了, 这时候整个乘法节点AST语法树就成了加号节点+ 的右节点了.

至此, 对于表达式 1 + 2 * 3 的AST语法树构建过程就完成了.
PrattParser节点升级
这时候, 我们再次拓展一下, 如果 1 + 2 * 3 + 5 会怎么样呢? 我们接着上一模块继续说, 基于第一个加法+, 整个PrattParser 仍然会往后寻找. 这时候会找到第二个加号+, 要考虑现在的优先级是最开始的优先级0, 所以加号的优先级高于0, 会继续执行.
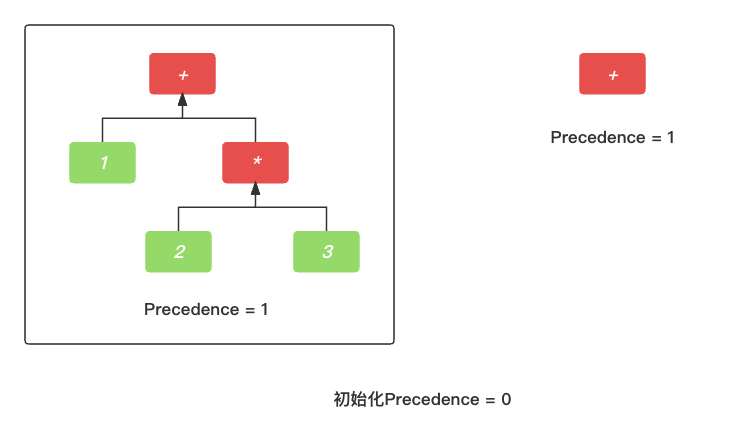
第一个加号 + 的AST语法树成为第二个加号 + 的左节点.
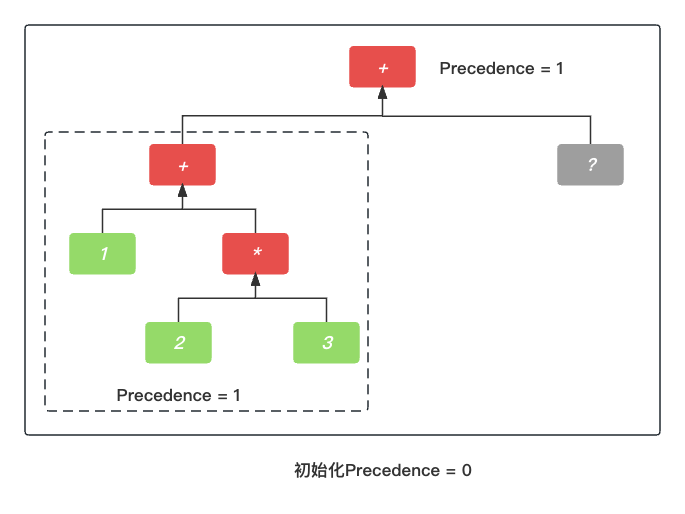
已发炮制, 继续查找第二个加号 + 的右节点.

最终, 1 + 2 * 3 + 5 的整体AST语法树就构建好了.

PrattParser的AST语法树优先级总结
结论只有这样的两点.
-
如果当前节点比先前节点的优先级高, 那么它会抢夺先前节点的右节点, 并把自己成为先前节点的右节点.
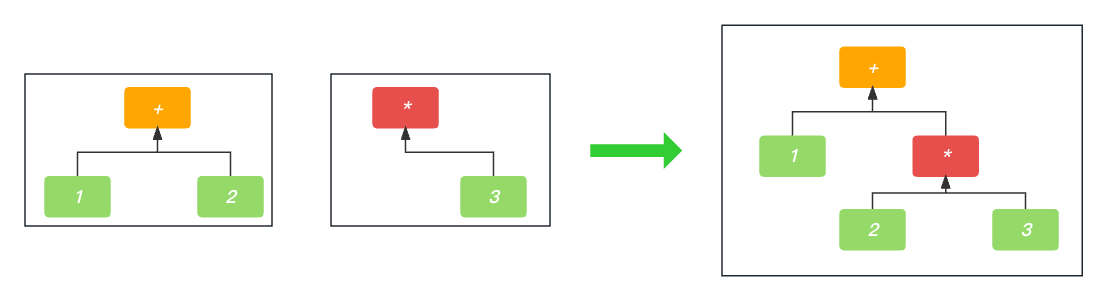
-
如果当前节点不比先前节点的优先级高, 那么它把先前节点当成自己的左节点.

总结
这一篇博客主要是说了以下 PrattParser解析器 的工作原理, 优先级等方面, 下一篇博客, 我会就着代码来逐步分析 PrattParser解析器 的实现过程. 如果有任何问题, 欢迎留言. 欢迎持续关注骚栋.








Comments | 0 条评论