![]()
2530. 执行 K 次操作后的最大分数
难度: 中等
来源: 每日一题 2023.10.18
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。你的 起始分数 为 0 。
在一步 操作 中:
选出一个满足 0 <= i < nums.length 的下标 i ,
将你的 分数 增加 nums[i] ,并且
将 nums[i] 替换为 ceil(nums[i] / 3) 。
返回在 恰好 执行 k 次操作后,你可能获得的最大分数。
向上取整函数 ceil(val) 的结果是大于或等于 val 的最小整数。
示例 1:
输入:nums = [10,10,10,10,10], k = 5
输出:50
解释:对数组中每个元素执行一次操作。最后分数是 10 + 10 + 10 + 10 + 10 = 50 。
示例 2:
输入:nums = [1,10,3,3,3], k = 3
输出:17
解释:可以执行下述操作:
第 1 步操作:选中 i = 1 ,nums 变为 [1,4,3,3,3] 。分数增加 10 。
第 2 步操作:选中 i = 1 ,nums 变为 [1,2,3,3,3] 。分数增加 4 。
第 3 步操作:选中 i = 2 ,nums 变为 [1,1,1,3,3] 。分数增加 3 。
最后分数是 10 + 4 + 3 = 17 。
提示:
1 <= nums.length, k <= 10^51 <= nums[i] <= 10^9
class Solution {
public long maxKelements(int[] nums, int k) {
}
}
分析与题解
-
暴力求解 时间超时, 失败
直接暴力法就是我们按照题意进行模拟运行, 每一次取完数组中的最后一个值就根据题意更新这个值, 然后重新排序整个数组.
long result = 0; for(int i = 0; i < k; i++) { int num = nums[nums.length - 1]; result += num; num = num/3 + (num%3 > 0 ? 1 : 0); nums[nums.length - 1] = num; Arrays.sort(nums); }整体的解题思路如下所示.
class Solution { public long maxKelements(int[] nums, int k) { Arrays.sort(nums); long result = 0; for(int i = 0; i < k; i++) { int num = nums[nums.length - 1]; result += num; num = num/3 + (num%3 > 0 ? 1 : 0); nums[nums.length - 1] = num; Arrays.sort(nums); } return result; } }
复杂度分析:
- 时间复杂度: O(klogn), 时间复杂度与
k相关, 排序需要损耗的时间复杂度为logn - 空间复杂度: O(klogn), 需要 k 次排序, 每一次都要消耗的空间复杂度为
logn
结果如下所示.

- 时间复杂度: O(klogn), 时间复杂度与
-
额外数组法
既然暴力排序的方式时间超时, 其原因就在于
Arrays.sort(nums);, 那我们就找一个不用排序的方式.我们发现, 当我们对
nums排序完成之后, 然后取出最后一位数据时, 并进行ceil(nums[i] / 3), 生成许多的item, 一定有这样的规律: 先生成的item一定不小于后生成的item的值.比如
[1, 10, 3, 3, 3]第一次是ceil(10 / 3) = 4, 第二次是ceil(4 / 3) = 2, 第三次是ceil(3 / 3) = 1, 结果是4 > 2 > 1, 结论是成立的.我们把这些
ceil(nums[i] / 3)生成的item单独并且依次放在一个数组removeNums中, 那么这个数组removeNums也是有序的.由于
nums不再删除数据了, 所以我们要用一个index记录当前nums中能取到的最大值.这时候取值过程就要分不同的逻辑分支了.
-
当
removeNums没有数据时, 我们就从nums中取最大值. 同时, index也需要偏移. 并且把ceil(nums[i] / 3)添加到removeNums中.
int num = nums[numsIndex]; result += num; removeNums.add(num/3 + (num%3 > 0 ? 1 : 0)); numsIndex--; -
当
removeNums有数据时, 我们就从nums中取最大值 和 从removeNums中取最大值, 两者取较大值. 当然了这时候还是需要更新removeNums的数据(删除最大值, 计算后放入数组尾部).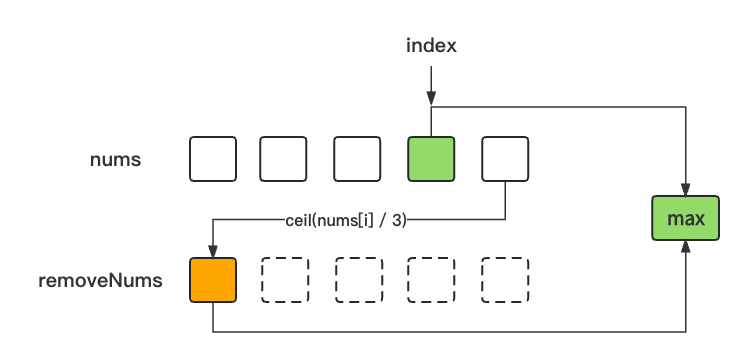
int num = removeNums.get(0); removeNums.remove(0); result += num; removeNums.add(num/3 + (num%3 > 0 ? 1 : 0));
接下来, 我们就一起看一下按照这个思路的整体的解题过程.
class Solution { public long maxKelements(int[] nums, int k) { Arrays.sort(nums); long result = 0; ArrayList<Integer> removeNums = new ArrayList<>(); int numsIndex = nums.length - 1; for(int i = 0; i < k; i++) { // 条件1: 如果 numsIndex 小于等于0 // 条件2: 如果当前removeNums有数据, 并且当前的removeNums的数据大于nums[numsIndex], 那就从removeNums中取出数据 // numsIndex 下标大于等于0是边界条件 if( numsIndex < 0 || (removeNums.size() != 0 && removeNums.get(0) > nums[numsIndex])) { int num = removeNums.get(0); removeNums.remove(0); result += num; removeNums.add(num/3 + (num%3 > 0 ? 1 : 0)); } else { int num = nums[numsIndex]; result += num; removeNums.add(num/3 + (num%3 > 0 ? 1 : 0)); numsIndex--; } } return result; } }
复杂度分析:
- 时间复杂度: O(k + logn), 遍历时间复杂度与
k相关, 排序需要损耗的时间复杂度为logn - 空间复杂度: O(logn), 排序消耗的空间复杂度为
logn
结果如下所示.

-
-
优先队列法
直接使用Java内置的优先队列
PriorityQueue, 这种方式我们不需要管理内部的排序逻辑, 直接通过PriorityQueue来完成.首先就是把所有的数据添加到优先队列中.
PriorityQueue<Integer> q = new PriorityQueue<Integer>((a, b) -> b - a); for (int num : nums) { q.offer(num); }然后就是通过
poll()取出最大值, 然后计算后再添加到优先队列中.long ans = 0; for (int i = 0; i < k; ++i) { int num = q.poll(); ans += num; q.offer(num/3 + (num%3 > 0 ? 1 : 0)); }接下来, 我们一起看一下整体的代码逻辑.
class Solution { public long maxKelements(int[] nums, int k) { PriorityQueue<Integer> q = new PriorityQueue<Integer>((a, b) -> b - a); for (int num : nums) { q.offer(num); } long ans = 0; for (int i = 0; i < k; ++i) { int num = q.poll(); ans += num; q.offer(num/3 + (num%3 > 0 ? 1 : 0)); } return ans; } }复杂度分析:
- 时间复杂度: O(nk), 遍历时间复杂度与
knums的长度相关 - 空间复杂度: O(n), 优先队列消耗的空间复杂度为
O(n)
结果如下所示.

- 时间复杂度: O(nk), 遍历时间复杂度与







Comments | 0 条评论