2652. 倍数求和

难度: 简单

来源: 每日一题 2023.10.17

---

给你一个正整数 n ，请你计算在 [1，n] 范围内能被 3、5、7 整除的所有整数之和。

返回一个整数，用于表示给定范围内所有满足约束条件的数字之和。

示例 1：

输入：n = 7
输出：21
解释：在 [1, 7] 范围内能被 3、5、7 整除的所有整数分别是 3、5、6、7 。数字之和为 21 。

示例 2：

输入：n = 10
输出：40
解释：在 [1, 10] 范围内能被 3、5、7 整除的所有整数分别是 3、5、6、7、9、10 。数字之和为 40 。

示例 3：

输入：n = 9
输出：30
解释：在 [1, 9] 范围内能被 3、5、7 整除的所有整数分别是 3、5、6、7、9 。数字之和为 30 。

提示：

• 1 <= n <= 10^3

class Solution {
    public int sumOfMultiples(int n) {

    }
}

分析与题解

---

• 遍历查找 + 暴力搜寻

  这个题目按照遍历查找好像没有啥难度, 就直接遍历查找符合题意的数字即可.

  整体逻辑代码如下所示.

  class Solution {
      public int sumOfMultiples(int n) {
          int result = 0;
          for(int i = 1; i <= n; i++) {
              if(i%3 == 0 || i%5 == 0 || i%7 == 0) {
                  result += i;
              }
          }
          return result;
      }
  }
  

  复杂度分析:

  • 时间复杂度: O(n), 一次遍历循环, 时间复杂度与n相关.
  • 空间复杂度: O(1), 常量级别的空间复杂度.

  结果如下所示.

  

• 等差数列 + 容斥原理

  首先说一下等差数列的概念, 对于这个题目来说就是从 1 - n中 所有能被 m 整除的和, 那我们知道, 会有如下的等差规律 m 2m 3m ... n/m * m, 求这个等差数列的和, 那么就如下所示.

  int sum = m + 2m + 3m + ... + n/m * m
  sum = (1 + 2 + 3 + n/m) * m
  sum = (1 + n/m) * (n/m) / 2 * m
  

  然后根据容次原理的相关内容.

  

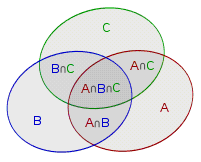
  我们可以得到 在 1 - n 中能被 3 , 5 , 7 整除的表达式如下所示.

  sun(n, 3) + sun(n, 5) + sun(n, 7) - sun(n, 3 * 5) - sun(n, 3 * 7) - sun(n, 5 * 7) + sun(n, 3 * 5 * 7);
  

  整体逻辑代码如下所示.

  class Solution {
      public int sun(int n, int m) {
          return (1 + n/m) * (n/m) / 2 * m;
      }
      public int sumOfMultiples(int n) {
          return sun(n, 3) + sun(n, 5) + sun(n, 7) - sun(n, 3 * 5) - sun(n, 3 * 7) - sun(n, 5 * 7) + sun(n, 3 * 5 * 7);
      }
  }
  

  复杂度分析:

  • 时间复杂度: O(1), 没有遍历, 常量级别的时间复杂度.
  • 空间复杂度: O(1), 常量级别的空间复杂度.

  结果如下所示.