617. 合并二叉树

难度: 简单

来源: 每日一题 2023.08.14

---

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

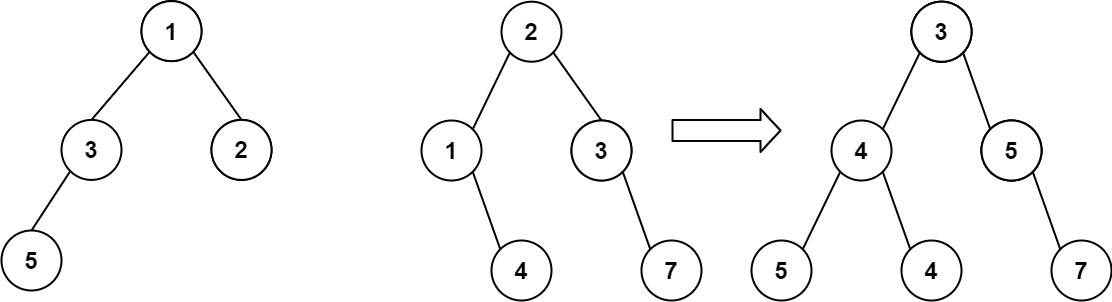
示例 1：

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

• 两棵树中的节点数目在范围 [0, 2000] 内

• -104 <= Node.val <= 104

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {

    }
}

分析与题解

---

• 重拳出击👊🏻 + 前/中/后序遍历任选其一遍历

  这个题目要求我们把两个二叉树合并在一起, 如果我们对前/中/后序遍历非常熟悉的话, 我们只需要通过一次递归性质的前/中/后序遍历即可完成整个题目.

  首先我们要先处理边界情况, 也就是 root1 和 root2 同时为空, 我们返回空.

  if (root1 == null && root2 == null) {
      return null;
  }
  

  然后就是创建当前node节点 把 root1 和 root2 的值添加到当前节点中.

  int value = 0;
  TreeNode node1Left = null, node1Right = null, node2Left = null, node2Right = null;
  
  if (root1 != null) {
      value += root1.val;
      node1Left = root1.left;
      node1Right = root1.right;
  }
  if (root2 != null) {
      value += root2.val;
      node2Left = root2.left;
      node2Right = root2.right;
  }
  TreeNode node = new TreeNode(value);
  

  最后我们对当前的 node节点的 left节点 和 right节点 进行递归操作即可.

  node.left = mergeTrees(node1Left, node2Left);
  node.right = mergeTrees(node1Right, node2Right);
  

  整个题目的题解过程如下所示.

  /**
  * Definition for a binary tree node.
  * public class TreeNode {
  *     int val;
  *     TreeNode left;
  *     TreeNode right;
  *     TreeNode() {}
  *     TreeNode(int val) { this.val = val; }
  *     TreeNode(int val, TreeNode left, TreeNode right) {
  *         this.val = val;
  *         this.left = left;
  *         this.right = right;
  *     }
  * }
  */
  class Solution {
      public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
          // 利用二叉树的前序遍历即可
          if (root1 == null && root2 == null) {
              return null;
          }
          int value = 0;
          TreeNode node1Left = null, node1Right = null, node2Left = null, node2Right = null;
  
          if (root1 != null) {
              value += root1.val;
              node1Left = root1.left;
              node1Right = root1.right;
          }
          if (root2 != null) {
              value += root2.val;
              node2Left = root2.left;
              node2Right = root2.right;
          }
          TreeNode node = new TreeNode(value);
          node.left = mergeTrees(node1Left, node2Left);
          node.right = mergeTrees(node1Right, node2Right);
          return node;
      }
  }
  

  复杂度分析:

  • 时间复杂度: O(max(m,n)), 谁多遍历谁.
  • 空间复杂度: O(min(m,n)), 谁的节点数量多就以谁为准, 当然了可能会超出.

  结果如下所示.